Выбор метода расчета лизинговых платежей

Материалы » Лизинговые операции коммерческих банкв » Выбор метода расчета лизинговых платежей

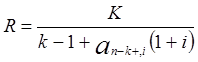. (3.7)

Теперь примем во внимание выплату аванса. Для лизинговых платежей постнумерандо соответственно получим

K = A+Ran,i ; K = A+Ran,i (+I),

откуда

R = (K-A)a, (3.8)

где коэффициент рассрочки определяется по формуле (3.4) и (3.5).

Если лизинговый контракт предусматривает выкуп имущества по остаточной стоимости, доля которой в стоимости имущества равна S, то получим следующее уравнение эквивалентных обязательств

.

Аналогично для выплат пренумерандо находим

(1+i).

Лизинговые платежи возмещают здесь стоимость оборудования за вычетом дисконтированной остаточной стоимости. Для расчета суммы платежа применяется формула

(3.9)

В случае, когда одновременно учитываются авансовый платеж и выкуп имущества, для последовательных платежей постнумерандо имеем

;

(1+i).

Соответственно получим

(3.10)

Рассмотрим пример управления лизинговыми платежами для ЗАО КБ «ПриватБанк». Условия лизинга следующие: К = 50 000 грн., n = 5 лет, I= 20%.

Размер лизингового платежа, рассчитанный по формуле (3.4) составит R = 16 717,39 грн.

В случае удвоенного взноса в конце первого года размер лизингового платежа рассчитывается по формуле (3.6) и составляет R= 14 611,05 грн. и первый взнос R1 = 29 222,1 грн.

Если предусмотрена выплата аванса А = 5 000 грн., то на основе (3.8) находим размер лизингового платежа, который составит R = 15 047,1 грн.

Если при прочих равных условиях предусматривается остаточная стоимость имущества S = 0,2, то размер лизингового платежа рассчитывается по формуле (3.9) и составляет

R = 15 375,2 грн.

При условии выплаты аванса А = 5 000 грн. и предусмотренной остаточной стоимости имущества S = 0,2 по формуле (3.10) находим R = 13 703,3 грн.

Условия погашения задолженности по лизингу могут предусматривать изменение платежей с постоянным темпом прироста k в каждом периоде. Иначе говоря, задается ускоренное, а иногда и замедленное погашение долга. Соответствующие платежи представляют собой ренту с постоянным относительным приростом. Размеры платежей рассчитываются следующим образом:

; t = 0,…, n-1. (3.11)

Темп прироста может быть положительной или отрицательной величиной. При этом k > 0 происходит ускорение погашения задолженности, при k < 0 – сокращение размеров платежей с каждым шагом во времени.

Размер первого платежа при условии полного погашения долга определяется как

R1 = K,

где b - коэффициент рассрочки для принятого порядка погашения долга. Рассчитывается по формуле:

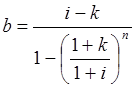(3.12)

Суммы погашения задолженности и величины остатка долга определяются последовательно по формулам:

, (3.13)

Другие материалы:

Структурные подразделения товарной биржи
Товарная биржа – это постоянно действующий организованный рынок оптовой купли-продажи массовых товаров или товаров народного потребления. Чаще всего в качестве объектов торговли на товарных биржах выступает сырьё и сельскохозяйственная продукция. Осуществлять сделки на товарной бирже могут лишь ее ...

Государственное регулирование рынка ценных бумаг
Государство на российском рынке ценных бумаг выступает в качестве: · эмитента при выпуске государственных ценных бумаг; · инвестора при управлении крупными портфелями акций промышленных предприятий. · профессионального участника при торговле акциями в ходе приватизационных аукционов; · регулятора п ...

Международные расчеты и валютные операции
Банк ВТБ является ведущим банком Украины в области обслуживания внешнеторговой деятельности, обязательства которого традиционно пользуются доверием в международных финансовых кругах. Поскольку Банк ВТБ является одним из немногих банков страны, аккредитивы и гарантии которого безусловно (т.е. без до ...