Выбор метода расчета лизинговых платежей

Материалы » Лизинговые операции коммерческих банкв » Выбор метода расчета лизинговых платежей

2. Во второй схеме рассчитываются размеры процентных платежей и суммы погашения долга (амортизация задолженности), затем определяется общая сумма лизингового платежа (в дальнейшем метод Б).

Различие между указанными методами не в существе, а в последовательности расчетных операций.

Для всех схем расчета исходным требованием является равенство современной стоимости потока лизинговых платежей затратам на приобретение оборудования, т.е. предусматривается финансовая эквивалентность обеих сторон контракта. В общем виде требование финансовой эквивалентности обязательств можно записать в виде следующего равенства:

, (3.1)

где К – стоимость имущества для банка-лизингодателя (с учетом таможенных сборов, страховых расходов и т.д.) без платы за кредит;

PV- оператор определения современной стоимости;

Rj – платежи по лизингу.

Формула (3.1) далее конкретизируется с учетом условий лизинга. В обсуждаемых методиках предполагается, что как при формировании потока платежей, так и при определении стоимости оборудования в них учитываются все налоговые выплаты.

В преобладающем числе случаев поток лизинговых платежей представляет собой постоянную ренту (метод А). Собственно методы расчетов периодических лизинговых платежей базируются на теории постоянных финансовых рент.

Для записи формул примем следующие обозначения:

R – размер постоянного платежа;

n – срок лизинга в месяцах, кварталах, годах (общее число платежей), как правило, в лизинговом контракте предусматривается число выплат платежей равное количеству начислений процентов;

i – процентная ставка за период (норма доходности);

S - доля остаточной стоимости в первоначальной стоимости оборудования;

аnij – коэффициент приведения постоянной ренты постнумерандо.

Если платежи погашают всю стоимость имущества, то развернув формулу (3.1), получим при выплатах постнумерандо

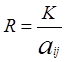(3.2)

Для упрощения расчетов платежей во многих случаях можно применить коэффициент рассрочки платежей, определяющий долю стоимости оборудования, погашаемую при каждой выплате:

. (3.3)

Коэффициент рассрочки для постоянных рент постнумерандо при условии, что применяются сложные проценты, равен а = 1/anij, то есть

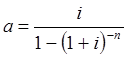. (3.4)

Коэффициент рассрочки для выплат пренумерандо составит:

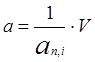, (3.5)

где V – дисконтный множитель по ставке i.

Если первый платеж будет в К раз больше остальных (удвоен или утроен), причем, соответственно сокращается число остальных платежей, тогда условие финансовой эквивалентности обязательств удовлетворится следующим равенствами:

Для выплат постнумерандо

.

для выплат пренумерандо

(1+I).

На основе этих равенств легко найти необходимые значения лизинговых платежей, а именно

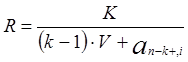, (3.6)

Другие материалы:

Современные тенденции торговых технологий
В наиболее общем виде торговые технологии могут быть классифицированы как технологии доступа на рынки и технологии организации этих рынков. Под технологиями доступа на рынки здесь понимаются программно- технологические средства, обеспечивающие участие в торгах на тех или иных финансовых рынках. Эти ...

Принципы деятельности коммерческого банка
Первым и основополагающим принципом деятельности коммерческого банка является работа в пределах реально имеющихся ресурсов. Коммерческий банк может осуществлять безналичные платежи в пользу других банков, предоставлять другим банкам кредиты и получать деньги наличными в пределах остатка средств на ...

Система гарантирования вкладов, как инструмент депозитной политики
Одной из важных мер, направленных на обеспечение надежности банковской системы в целом и каждого конкретного банка, является создание механизмов сохранности вкладов физических лиц. В международной практике такой механизм называется страхование депозитов. Оно применяется в странах с хорошо развитой ...